An Introduction to Genetic Algorithms

Introduction

Nowadays we all should be familiar with the process o evolution by natural selection. I’m not an expert, but we can summarise it as “random mutations and natural selection bring to the survival of the fittest”.

Imagine applying this to a search or optimization problem: you start with a random solution and let the principles of evolution find the best set of parameters to solve the problem.

How can we simulate the evolution of an encoded solution?
Is it always going to find the best solution?
Why should I choose this technique?
Let’s go deeper!

Genetic Algorithm in a Nutshell

First, we need a population. (but a population of what?)
We can assume, and it shouldn't be too difficult, that the way our solution is encoded is a binary string, let’s call it a chromosome.

Now we can have an initial set of chromosomes, we can hardcode it or we can generate them randomly, at this point it’s not very important, but let’s call this our population.

the initial population

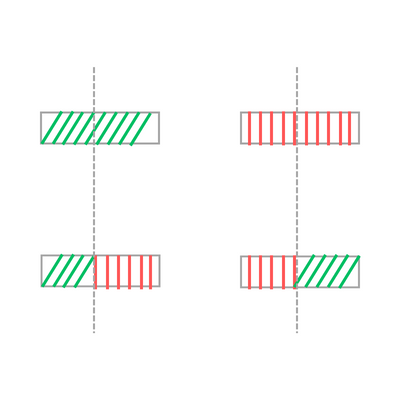
Now we need a way to modify the population gradually, let’s introduce the operation crossover. Given two chromosomes we randomly pick an index that divides both of them into two parts, we now take the first part of the first chromosome and combine it with the second part of the second chromosome and vice-versa!

One-point Crossover

This operation is called one-point crossover because we select just one random index, we can use a two-point or k-point crossover, as you can imagine there are many different variations of this operation, but the critical insight is that you create two new chromosomes that could, in theory, take the best out of the parent's chromosomes and give you better results.

We also define a random mutation, we can set a probability p of mutation of a given resulting chromosome, in practice negating a random bit, this should explore new directions leading us to new solutions.

To finish our genetic algorithm we need one last thing, a function that tests a given genome and gives us the fittest value, namely how well this chromosome solves our problem.

Given all these little pieces we can generalize GAs as follows:

1. Initialize a population P

2. Find a new population Q using crossover

3. Using F as the fittest function, remove from Q the worst k chromosomes and add to Q the best k chromosomes from P

4. Set Q as your population and repeat from point 2.

We can stop after a certain number of epochs and/or set a certain fittest value on which we would like to stop.

---

A Genetic solution to the Knapsack problem

For those that are not familiar with the Knapsack problem:

Given a set of items, each with a weight and a value, determine which items to include in the collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.

Let’s define the max weight for our knapsack and the list of items. In this case, the solution is trivial, if we take the first item and the last one we achieve a weight of 17 and the value 36 that is the max that we can achieve with this input.

import random

class Item:
  def __init__(self, value, weight):
    self.value = value
    self.weight = weight


if __name__ == "__main__":
  MAX_WEIGHT = 20
  items = [
      Item(12, 5),
      Item(7, 5),
      Item(9, 16),
      Item(10, 4),
      Item(24, 12)
  ]

We need a way to randomly initialise our population and encode our solutions. I’m using the following encoding: chromosome [1, 0, 1, 1] indicates that we must take the first element and the last two, so 1 at index j means take item j, chromosome_size is going to be the number of items.

def init_population(count, chromosome_size):
  population = []
  for _ in range(count):
    population.append(
      [random.randint(0,1) for _ in range(chromosome_size)]
    )
  return population

I implemented a one-point crossover operation; in this case, the index can also be the first or last index, which means that the children will be equal to the parents, which can be useful in some cases.
The fittest function sums the value of the items that a specific chromosome selects, if the weight is over the max_weight we set its fittest value to 0 otherwise to the total value.

def crossover(a, b):
  index = random.randint(0, len(a)-1)
  child1 = a[:index] + b[index:]
  child2 = b[:index] + a[index:]
  return child1, child2

def fittest(chromosome, items, max_weight):
  total_value = sum(
    chromosome[i]*item.value for i, item in enumerate(items)
  )
  total_weight = sum(
    chromosome[i]*item.weight for i, item in enumerate(items)
  )
  return 0 if total_weight>max_weight else total_value

To create a new population I simply use the crossover function to create new chromosomes, then apply a random mutation (I set a really high frequency of mutations, it needs to be tuned on the specific problem) then I remove the worst chromosome of the new population and add the best chromosome of the previous population

def new_population(population, items, max_weight):
  random.shuffle(population)
  new = []

  for i in range(0, len(population)-1, 2):
    child1, child2 = crossover(population[i], population[i+1])
    new.append(child1)
    new.append(child2)
  
  if random.randint(1, 100) < 10:
    index = random.randint(0, len(new)-1)
    gene = random.randint(0, len(new[0])-1)
    new[index][gene] = new[index][gene] ^ 1

  new.remove(
    min(new, key=lambda x: fittest(x, items, max_weight))
  ) 
  
  new.append(
    max(population, key=lambda x: fittest(x, items, max_weight))
  )
  
  for chromosome in new:
    fittest_value = fittest(chromosome, items, max_weight)
    print(f"chromosome :: {chromosome} with fittest value :: {fittest_value}")
  return new

The complete main:

if __name__ == "__main__":
  MAX_WEIGHT = 20
  items = [
    Item(12, 5),
    Item(7, 5),
    Item(9, 16),
    Item(10, 4),
    Item(24, 12)
  ]
  
  population = init_population(7, len(items))
  for epoch in range(20):
    print(f"Epoch :: {epoch}")
    population = new_population(population, items, MAX_WEIGHT)
    print("-"*20)

Conclusion

This was a brief introduction to GAs, there are different algorithms that use this simple concept for Neural Networks for example. When I first learnt about this I asked myself Why don’t we use it everywhere?

Why should we use GAs?

• are really easy to code

• gives many solutions so can avoid local extrema

• can be parallelized

Why shouldn’t we?

• random heuristics sometimes does not find the optimum or is very slow in doing so

• fitness function may not be easily designed

In conclusion, they are just another tool in our belt. Let us always remember to choose tools according to the problem to be solved and not according to what we like.